Convex Hull
Brandon Blatter
CS 312
View this report in your browser
Let's be honest. PDFs were not meant for displaying code, and code was not meant to be displayed in PDFs. Please view this report in your browser so it's easy to read.
Code
ConvexHull.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Drawing;
namespace _1_convex_hull {
public class ConvexHull {
public ConvexHull() {
// set empty list
hullPoints = new List<PointF>();
}
public ConvexHull(List<PointF> singleList) {
// set list—used for one or two point lists
hullPoints = singleList;
rightmostIndex = singleList.Count - 1;
}
// used for storing the result of joining hulls
public ConvexHull(List<PointF> pointList, int newRightmostIndex) {
// set points
hullPoints = pointList;
// initialize rightmost index
rightmostIndex = newRightmostIndex;
}
private List<PointF> hullPoints;
private int rightmostIndex;
public PointF GetPointByIndex(int index) {
return hullPoints[index];
}
public int GetRightmostIndex() {
// the rightmost index will always be zero
return rightmostIndex;
}
public int GetLeftmostIndex() {
// the leftmost index is stored and maintained for convenience
return 0;
}
// gets the next clockwise index
public int GetNextCWIndex(int currentIndex) {
// if zero isn't reached yet, return the next index in sequence
if(currentIndex < hullPoints.Count - 1) return currentIndex + 1;
// otherewise return the first index
else return 0;
}
// gets the next counter-clockwise index
public int GetNextCCWIndex(int currentIndex) {
// if the current index is zero, return the last index in the list
if(currentIndex == 0) return hullPoints.Count - 1;
// otherwise return the next index in sequence
else return currentIndex - 1;
}
// returns the list of points
public List<PointF> GetPoints() {
return hullPoints;
}
}
}
ConvexHullSolver.cs
using System;
using System.Collections.Generic;
using System.Text;
using System.Drawing;
using System.Linq;
using System.Threading;
using _1_convex_hull;
namespace _2_convex_hull {
class ConvexHullSolver {
bool vis;
int delayTime;
Graphics g;
Pen blackPen;
Pen redPen;
Pen bluePen;
Pen whitePen;
SolidBrush greenBrush;
SolidBrush orangeBrush;
Font font;
System.Windows.Forms.PictureBox pictureBoxView;
public ConvexHullSolver(Graphics g, System.Windows.Forms.PictureBox pictureBoxView) {
vis = false;
delayTime = 800;
this.g = g;
this.blackPen = new Pen(Color.Black);
this.redPen = new Pen(Color.Red);
this.bluePen = new Pen(Color.Blue);
this.whitePen = new Pen(Color.White);
this.greenBrush = new SolidBrush(Color.Green);
this.orangeBrush = new SolidBrush(Color.Orange);
this.font = new Font("Helvetica", 16);
this.pictureBoxView = pictureBoxView;
}
public void Refresh() {
// Use this especially for debugging and whenever you want to see what you have drawn so far
pictureBoxView.Refresh();
}
public void Pause(int milliseconds) {
// Use this especially for debugging and to animate your algorithm slowly
pictureBoxView.Refresh();
Thread.Sleep(milliseconds);
pictureBoxView.Refresh();
}
private double CalcSlope(PointF point1, PointF point2) {
return (point2.Y - point1.Y) / (point2.X - point1.X);
}
private int GetHighestCCWLeftIndex(ConvexHull leftHull, ConvexHull rightHull, int leftIndex, int rightIndex) {
PointF leftPoint = leftHull.GetPointByIndex(leftIndex);
PointF rightPoint = rightHull.GetPointByIndex(rightIndex);
int nextLeftIndex = leftHull.GetNextCCWIndex(leftIndex);
PointF nextLeftPoint = leftHull.GetPointByIndex(nextLeftIndex);
// compare slopes
if(CalcSlope(nextLeftPoint, rightPoint) > CalcSlope(leftPoint, rightPoint)) {
// if new slope is smaller, try to get a higher left point
return GetHighestCCWLeftIndex(leftHull, rightHull, nextLeftIndex, rightIndex);
} else {
// if new slope is larger, return this left point
return leftIndex;
}
}
private int GetHighestCWRightIndex(ConvexHull leftHull, ConvexHull rightHull, int leftIndex, int rightIndex) {
PointF leftPoint = leftHull.GetPointByIndex(leftIndex);
PointF rightPoint = rightHull.GetPointByIndex(rightIndex);
int nextRightIndex = rightHull.GetNextCWIndex(rightIndex);
PointF nextRightPoint = rightHull.GetPointByIndex(nextRightIndex);
// compare slopes
if(CalcSlope(leftPoint, nextRightPoint) < CalcSlope(leftPoint, rightPoint)) {
// if new slope is smaller, try to get a higher right point
return GetHighestCWRightIndex(leftHull, rightHull, leftIndex, nextRightIndex);
} else {
// if new slope is larger, return this right point
return rightIndex;
}
}
private int GetLowestCWLeftIndex(ConvexHull leftHull, ConvexHull rightHull, int leftIndex, int rightIndex) {
PointF leftPoint = leftHull.GetPointByIndex(leftIndex);
PointF rightPoint = rightHull.GetPointByIndex(rightIndex);
int nextLeftIndex = leftHull.GetNextCWIndex(leftIndex);
PointF nextLeftPoint = leftHull.GetPointByIndex(nextLeftIndex);
// compare slopes
if(CalcSlope(nextLeftPoint, rightPoint) < CalcSlope(leftPoint, rightPoint)) {
// if new slope is larger, try to get a lower left point
return GetLowestCWLeftIndex(leftHull, rightHull, nextLeftIndex, rightIndex);
} else {
// if new slope is smaller, return this left point
return leftIndex;
}
}
private int GetLowestCCWRightIndex(ConvexHull leftHull, ConvexHull rightHull, int leftIndex, int rightIndex) {
PointF leftPoint = leftHull.GetPointByIndex(leftIndex);
PointF rightPoint = rightHull.GetPointByIndex(rightIndex);
int nextRightIndex = rightHull.GetNextCCWIndex(rightIndex);
PointF nextRightPoint = rightHull.GetPointByIndex(nextRightIndex);
// compare slopes
if(CalcSlope(leftPoint, nextRightPoint) > CalcSlope(leftPoint, rightPoint)) {
// if new slope is smaller, try to get a lower right point
return GetLowestCCWRightIndex(leftHull, rightHull, leftIndex, nextRightIndex);
} else {
// if new slope is larger, return this right point
return rightIndex;
}
}
private ConvexHull JoinHulls(ConvexHull leftHull, ConvexHull rightHull) {
if(vis) {
LabelPoints(leftHull.GetPoints(), greenBrush);
LabelPoints(rightHull.GetPoints(), orangeBrush);
}
// get closest points
int leftHullClosestIndex = leftHull.GetRightmostIndex();
int rightHullClosestIndex = rightHull.GetLeftmostIndex();
int tempLeft, tempRight;
bool leftDone;
bool rightDone;
// find upper common tangent
// compare slopes CCW up left and CW up right
int highestCCWLeftIndex = leftHullClosestIndex;
int highestCWRightIndex = rightHullClosestIndex;
// keep trying to find higher points until we break
while(true) {
rightDone = false;
leftDone = false;
if(vis) {
g.DrawLine(whitePen, leftHull.GetPointByIndex(highestCCWLeftIndex), rightHull.GetPointByIndex(highestCWRightIndex));
}
// get the next highest left point and update
tempLeft = GetHighestCCWLeftIndex(leftHull, rightHull, highestCCWLeftIndex, highestCWRightIndex);
leftDone = (tempLeft == highestCCWLeftIndex);
highestCCWLeftIndex = tempLeft;
// get the next highest right point and update
tempRight = GetHighestCWRightIndex(leftHull, rightHull, highestCCWLeftIndex, highestCWRightIndex);
rightDone = (tempRight == highestCWRightIndex);
highestCWRightIndex = tempRight;
if(vis) {
g.DrawLine(redPen, leftHull.GetPointByIndex(highestCCWLeftIndex), rightHull.GetPointByIndex(highestCWRightIndex));
}
// if neither point can be lowered, break out of the loop
if(leftDone && rightDone) break;
}
// find lower common tangent
// compare slopes CW down left and CCW down right
int lowestCWLeftIndex = leftHullClosestIndex;
int lowestCCWRightIndex = rightHullClosestIndex;
// keep trying to find higher points until we break
while(true) {
rightDone = false;
leftDone = false;
if(vis) {
g.DrawLine(whitePen, leftHull.GetPointByIndex(lowestCWLeftIndex), rightHull.GetPointByIndex(lowestCCWRightIndex));
}
// get the next lowest left point and update
tempLeft = GetLowestCWLeftIndex(leftHull, rightHull, lowestCWLeftIndex, lowestCCWRightIndex);
leftDone = (tempLeft == lowestCWLeftIndex);
lowestCWLeftIndex = tempLeft;
// get the next lowest right point and update
tempRight = GetLowestCCWRightIndex(leftHull, rightHull, lowestCWLeftIndex, lowestCCWRightIndex);
rightDone = (tempRight == lowestCCWRightIndex);
lowestCCWRightIndex = tempRight;
if(vis) {
g.DrawLine(bluePen, leftHull.GetPointByIndex(lowestCWLeftIndex), rightHull.GetPointByIndex(lowestCCWRightIndex));
}
// if neither point can be lowered, break out of the loop
if(leftDone && rightDone) break;
}
// join three segments of hulls together
List<PointF> joinedHullPoints = new List<PointF>();
// add from 0 to high left from left hull
for (int i = 0; i != highestCCWLeftIndex; i = leftHull.GetNextCWIndex(i)) {
joinedHullPoints.Add(leftHull.GetPointByIndex(i));
}
// add highest left point from left hull
joinedHullPoints.Add(leftHull.GetPointByIndex(highestCCWLeftIndex));
// add from highest right to lowest right from right hull
for (int i = highestCWRightIndex; i != lowestCCWRightIndex; i = rightHull.GetNextCWIndex(i)) {
joinedHullPoints.Add(rightHull.GetPointByIndex(i));
}
// add lowest right point from right hull
joinedHullPoints.Add(rightHull.GetPointByIndex(lowestCCWRightIndex));
// add from low left to 0 from left hull
for (int i = lowestCWLeftIndex; i != 0; i = leftHull.GetNextCWIndex(i)) {
joinedHullPoints.Add(leftHull.GetPointByIndex(i));
}
// get the new rightmost index
int newRightmostIndex = highestCCWLeftIndex + (rightHull.GetRightmostIndex() - highestCWRightIndex) + 1;
ConvexHull joinedHull = new ConvexHull(joinedHullPoints, newRightmostIndex);
return joinedHull;
}
private ConvexHull FindConvexHull(List<PointF> pointList) {
int numItems = pointList.Count;
// base case; in either of these cases the hull will always be correct
if(numItems == 1 || numItems == 2) return new ConvexHull(pointList);
// recur down to find the sub hulls
ConvexHull leftHull = FindConvexHull(new List<PointF>(pointList.Take(numItems / 2)));
ConvexHull rightHull = FindConvexHull(new List<PointF>(pointList.Skip(numItems / 2)));
// join the two hulls together
ConvexHull finalHull = JoinHulls(leftHull, rightHull);
return finalHull;
}
public void LabelPoints(List<PointF> pointList, SolidBrush brush) {
for (int i = 0; i < pointList.Count; i++) {
g.DrawString(i.ToString(), font, brush, pointList[i]);
}
}
public void ListPoints(List<PointF> pointList) {
for (int i = 0; i < pointList.Count; i++) {
Console.WriteLine(pointList[i]);
}
}
public void DrawList(List<PointF> pointList) {
for(int i = 0; i < pointList.Count - 1; i++) {
g.DrawLine(blackPen, pointList[i], pointList[i + 1]);
}
g.DrawLine(blackPen, pointList[pointList.Count - 1], pointList[0]);
}
public void Solve(List<PointF> pointList) {
// sort points
pointList = pointList.OrderBy(o=>o.X).ToList();
// call recursive function
ConvexHull finalHull = FindConvexHull(pointList);
DrawList(finalHull.GetPoints());
}
}
}
Complexity
Time Complexity
- Sort points by X value: O(n log n)
- Recur log2 times for a big O of O(log n) and perform O(n) operations as follows at each level: O(n log n)
- Divide into sub hulls: O(1)
- Find the upper and lower common tangents: O(n)
- Join sub hulls: O(n)
Steps 1 and 2 are both O(n log n) so the final time complexity is O(n log n) (Step 2 is repeated log n times and each repetition has a big O of O(n) because in the worst case every point will be touched at each level of the recursion).
The time complexity of this project can also be estimated using the Master Theorem.
This divide and conquer implementation of the convex hull problem divides the original list of points with a size of "n" into "a" sub-problems of size "b" at each level. The depth of the branching tree is log2n. The big O of combining the two sub-hulls is n1 where "n" is the size of the original hull. We have the following values:
a = 2
b = 2
d = 1
Which give us the following ratio:
2 / 21 = 2 / 2 = 1
According to the Master Theorem, this ratio means the big O of each of the O(log n) terms is O(nd) = O(n1) = O(n). The final big O for the entire algorithm is then O(n log n).
Space Complexity
Assuming all of the convex hull objects are kept in memory until the program terminates, it will end up having a space complexity of O(n log n). This is because at each of the log n levels of the recursion tree the convex hull objects will take up O(n) space. New convex hulls objects are created at each level. This space complexity could be improved if one of the convex hulls being combined was used as the new convex hull rather than being replaced by it.
Outcomes
Raw
| 10 | 100 | 1000 | 10000 | 100000 | 500000 | 1000000 |
|---|---|---|---|---|---|---|
| 0.02939 | 0.01264 | 0.01743 | 0.04470 | 0.34600 | 1.73135 | 3.54511 |
| 0.02166 | 0.01477 | 0.01522 | 0.04724 | 0.34228 | 1.69787 | 3.45634 |
| 0.01261 | 0.01445 | 0.01738 | 0.04538 | 0.35544 | 1.69251 | 3.47596 |
| 0.01240 | 0.01329 | 0.01530 | 0.04686 | 0.35048 | 1.68295 | 3.56687 |
| 0.01365 | 0.01389 | 0.01620 | 0.04278 | 0.33587 | 1.70093 | 3.50649 |
Times recorded are in seconds.
Mean
| 10 | 100 | 1000 | 10000 | 100000 | 500000 | 1000000 |
|---|---|---|---|---|---|---|
| 0.01794 | 0.01381 | 0.01631 | 0.04539 | 0.34601 | 1.70112 | 3.51015 |
Times recorded are in seconds.
Graphs
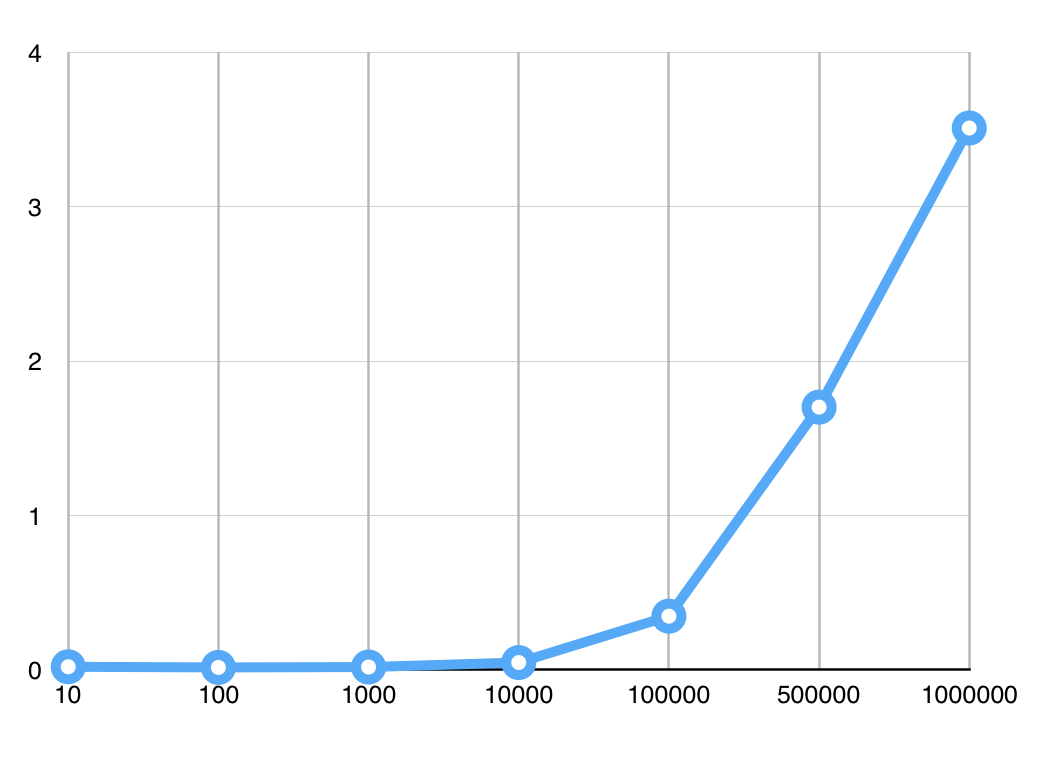
This graph roughly has the shape of an n log n function. The only discrepancy is the 500000 value—if removed, the graph would appear to grow more normally. If it grew as a function of log10 the graph shown here would be straight with an incline. However, log n multiplied by n gives the slope an extra curve upward.
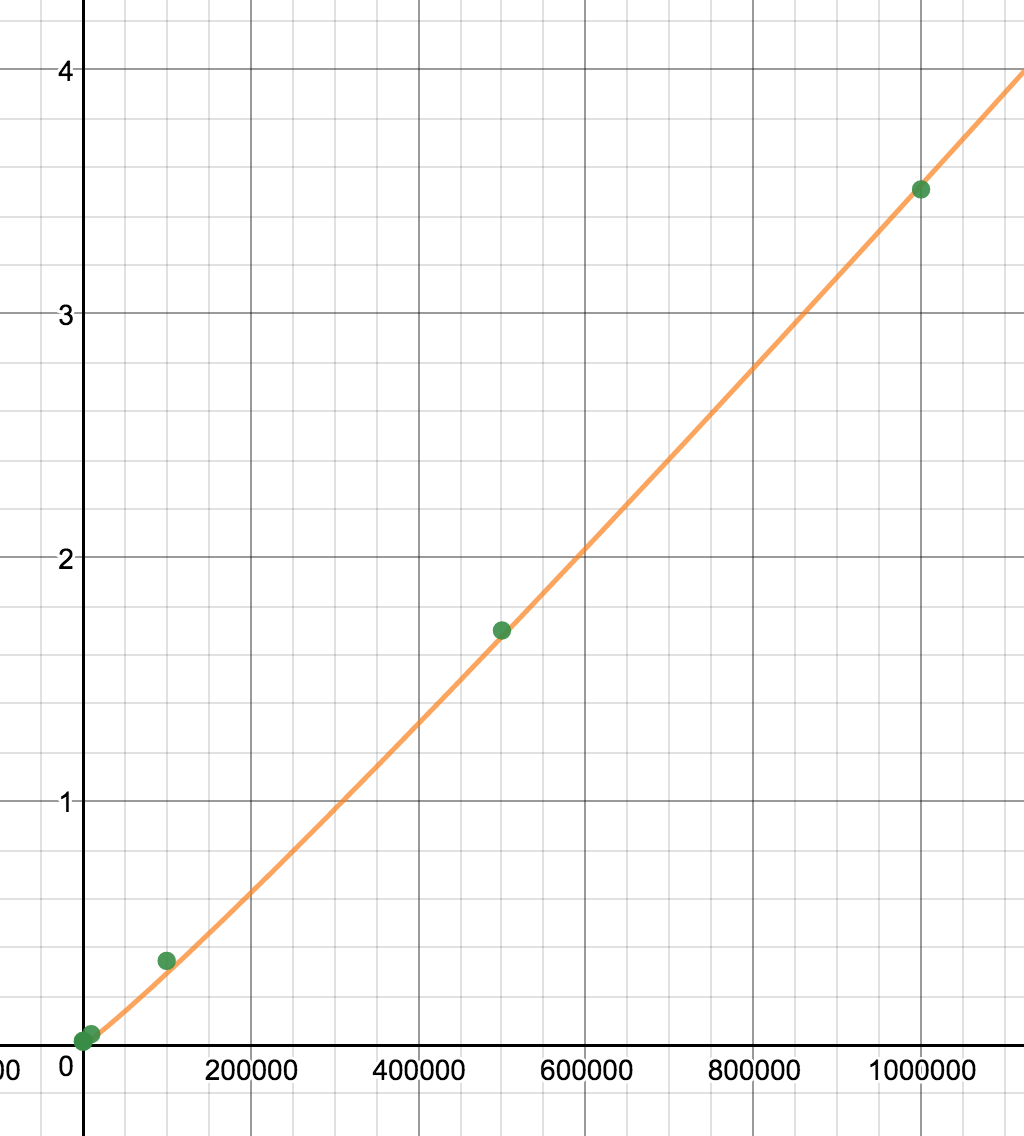
This graph shows a to-scale representation of the data. I was able to fit a regression line to this data with the following equation:
y = 5.878 * 10-7 x log x
In this equation, y is the time and x = n. The constant of proportionality is 5.878 * 10-7. This constant is so small because a plain time = n log n would yield a time of about 23 seconds for a list of 10 points. My computer processor is much faster than that, hence the constant of proportionality.
Observations
Besides the constant of proportionality factor, the graphs appear to closely match the expected n log n outcome. What's interesting to note is that this complexity is about the same for both the uniform distribution and the Gaussian distribution. However, the final convex hull of a Gaussian distribution with more than 1000000 points still only consists of a few points, which suggests that this algorithm is not efficient at all for Gaussian distributions. For comparison, a human might be able to beat a desktop computer in finding the convex hull given a set of 1000000000 points or so if the divide and conquer method is used.
Screenshots
100 points
1000 points