Network Routing
Brandon Blatter
CS 312
View this report in your browser
Let's be honest. PDFs were not meant for displaying code, and code was not meant to be displayed in PDFs. Please view this report in your browser so it's easy to read.
Code
NetworkPoint.cs
using System;
using System.Collections.Generic;
using System.Drawing;
namespace NetworkRouting
{
// custom class that manages data associated with each node
public class NetworkPoint
{
public NetworkPoint(PointF p, int index)
{
point = p;
listIndex = index;
prevPoint = null;
distance = 1000000000;
}
public PointF point;
public int listIndex;
public NetworkPoint prevPoint;
public double distance;
}
}
NetworkSolver.cs
using System;
using System.Collections.Generic;
using System.Drawing;
namespace NetworkRouting
{
public class NetworkSolver
{
public NetworkSolver(int start, int stop, List<PointF> points, List<HashSet<int>> adjacencies)
{
startNodeIndex = start;
stopNodeIndex = stop;
pointList = new List<NetworkPoint>();
// initialize point list
for(int i = 0; i < points.Count; i++) {
pointList.Add(new NetworkPoint(points[i], i));
}
// set start node to have a distance of 0
pointList[startNodeIndex].distance = 0;
adjacencyList = adjacencies;
}
private int startNodeIndex;
private int stopNodeIndex;
private List<NetworkPoint> pointList;
private List<HashSet<int>> adjacencyList;
private BinaryHeapPQ binaryHeapH;
private ArrayPQ arrayH;
private List<PointF> getStopToStartList(NetworkPoint stopPoint) {
NetworkPoint currentPoint = stopPoint;
List<PointF> points = new List<PointF>();
while(currentPoint.listIndex != startNodeIndex) {
points.Add(currentPoint.point);
currentPoint = currentPoint.prevPoint;
}
points.Add(currentPoint.point);
return points;
}
private double DistanceBetween(NetworkPoint point1, NetworkPoint point2) {
double xDistance = point1.point.X - point2.point.X;
double yDistance = point1.point.Y - point2.point.Y;
return Math.Sqrt(xDistance * xDistance + yDistance * yDistance);
}
public List<PointF> SolveWithBinaryHeap() {
// constructor will run setup and MakeQueue
binaryHeapH = new BinaryHeapPQ(pointList);
NetworkPoint u = null;
HashSet<int> adjacentToU = null;
NetworkPoint v = null;
// Dijkstra's algorithm
while(!binaryHeapH.IsEmpty()) {
u = binaryHeapH.DeleteMin();
// points not connected - report error
if(u == null) return null;
if(u.listIndex == stopNodeIndex) return getStopToStartList(u);
// get adjacent point indices
adjacentToU = adjacencyList[u.listIndex];
foreach(int adjacentIndex in adjacentToU) {
// process point
v = pointList[adjacentIndex];
if(v.distance > u.distance + DistanceBetween(u, v)) {
v.distance = u.distance + DistanceBetween(u, v);
v.prevPoint = u;
binaryHeapH.DecreaseKey(v.listIndex);
}
}
}
// stop point not found (should never execute)
return null;
}
public List<PointF> SolveWithArray() {
// constructor will run setup and MakeQueue
arrayH = new ArrayPQ(pointList);
NetworkPoint u = null;
HashSet<int> adjacentToU = null;
NetworkPoint v = null;
// Dijkstra's algorithm
while(!arrayH.IsEmpty()) {
u = arrayH.DeleteMin();
// points not connected - report error
if(u == null) return null;
if(u.listIndex == stopNodeIndex) return getStopToStartList(u);
// get adjacent point indices
adjacentToU = adjacencyList[u.listIndex];
foreach(int adjacentIndex in adjacentToU) {
// process point
v = pointList[adjacentIndex];
if(v.distance > u.distance + DistanceBetween(u, v)) {
v.distance = u.distance + DistanceBetween(u, v);
v.prevPoint = u;
arrayH.DecreaseKey(v.listIndex);
}
}
}
// stop point not found (should never execute)
return null;
}
}
}
ArrayPQ.cs
using System;
using System.Collections.Generic;
using System.Drawing;
namespace NetworkRouting
{
public class ArrayPQ
{
public ArrayPQ(List<NetworkPoint> points)
{
MakeQueue(points);
}
private List<NetworkPoint> pointList;
public bool IsEmpty() {
return pointList.Count == 0;
}
// MakeQueue: O(n)
public void MakeQueue(List<NetworkPoint> points) {
// reset list of points
pointList = new List<NetworkPoint>();
// add each point given; order doesn't matter
for (int i = 0; i < points.Count; i++) {
Insert(points[i]);
}
}
// Insert: O(1)
public void Insert(NetworkPoint point) {
// initialize point with default values
pointList.Add(point);
}
// DeleteMin: O(n)
public NetworkPoint DeleteMin() {
double minDistance = 1000000000;
NetworkPoint min = null;
int mindex = -1;
// find point with smallest distance
for (int i = 0; i < pointList.Count; i++) {
if(pointList[i].distance != -1 && pointList[i].distance < minDistance) {
minDistance = pointList[i].distance;
min = pointList[i];
mindex = i;
}
}
// if all points are unreachable
if(min == null) return null;
// remove min from list
pointList.RemoveAt(mindex);
// return that point so it can be used
return min;
}
// Insert: O(1)
public void DecreaseKey(int index) {
// do nothing - no change in array implementation
}
}
}
BinaryHeapPQ.cs
using System;
using System.Collections.Generic;
using System.Drawing;
namespace NetworkRouting
{
public class BinaryHeapPQ
{
public BinaryHeapPQ(List<NetworkPoint> points)
{
MakeQueue(points);
}
// locations of nodes on the heap (access from DeleteMin)
private List<int> heapLocations;
private List<NetworkPoint> heapList;
public bool IsEmpty() {
return heapList.Count == 0;
}
// gets node's parent from binary heap by index
private int GetParentIndex(int nodeIndex) {
return nodeIndex / 2;
}
private int GetSmallerChildIndex(int nodeIndex) {
int childIndex1 = nodeIndex * 2;
// if left child index is greater than size of heap, use nodeIndex
if(childIndex1 >= heapList.Count) return nodeIndex;
int childIndex2 = childIndex1 + 1;
// if right child index is greater than size of heap, use left child index
if(childIndex2 >= heapList.Count) return childIndex1;
NetworkPoint child1 = heapList[childIndex1];
NetworkPoint child2 = heapList[childIndex2];
// if right child doesn't exist or has greater distance, use left child
if(child1.distance < child2.distance) return childIndex1;
// otherwise use right child
else return childIndex2;
}
// swap nodes by index in heap list
private void SwapNodes(int nodeIndex1, int nodeIndex2) {
// get nodes to switch
NetworkPoint node1 = heapList[nodeIndex1];
NetworkPoint node2 = heapList[nodeIndex2];
// swap nodes actual nodes in heapList
heapList[nodeIndex2] = node1;
heapList[nodeIndex1] = node2;
// swap indices in heapLocations
heapLocations[node1.listIndex] = nodeIndex2;
heapLocations[node2.listIndex] = nodeIndex1;
}
private void BubbleUp(int nodeIndex) {
int parentIndex = GetParentIndex(nodeIndex);
// while parent value is higher
while(heapList[parentIndex].distance > heapList[nodeIndex].distance) {
// swap nodes
SwapNodes(parentIndex, nodeIndex);
// update current node and parent indices
nodeIndex = parentIndex;
parentIndex = GetParentIndex(parentIndex);
}
}
private void BubbleDown(int nodeIndex) {
int smallerChildIndex = GetSmallerChildIndex(nodeIndex);
if(smallerChildIndex == 0) return;
// while child value is lower
while(heapList[smallerChildIndex].distance < heapList[nodeIndex].distance) {
// swap nodes
SwapNodes(smallerChildIndex, nodeIndex);
// update current node and parent indices
nodeIndex = smallerChildIndex;
smallerChildIndex = GetSmallerChildIndex(smallerChildIndex);
if(smallerChildIndex == 0) return;
}
}
// MakeQueue: O(n log n)
public void MakeQueue(List<NetworkPoint> points) {
// reset list of points
heapList = new List<NetworkPoint>();
heapLocations = new List<int>();
// add each point given; order doesn't matter
for (int i = 0; i < points.Count; i++) {
Insert(points[i]);
}
}
// Insert: O(log n)
public void Insert(NetworkPoint point) {
// add point to end of list (bottom right of tree)
heapList.Add(point);
// add location as the last element in the heap list
heapLocations.Add(heapList.Count - 1);
// bubble up
BubbleUp(heapList.Count - 1);
}
// DeleteMin: O(log n)
public NetworkPoint DeleteMin() {
// if top node is greater than our cutoff, assume unreachable
if(heapList[0].distance > 999999999) return null;
// get top node
NetworkPoint min = heapList[0];
heapLocations[min.listIndex] = -1;
// replace top node with bottommost rightmost
heapList[0] = heapList[heapList.Count - 1];
heapList.RemoveAt(heapList.Count - 1);
if(heapList.Count > 0) {
heapLocations[heapList[0].listIndex] = 0;
}
// bubble down
BubbleDown(0);
return min;
}
// DecreaseKey: O(log n)
public void DecreaseKey(int listIndex) {
// bubble up actual location in heap
BubbleUp(heapLocations[listIndex]);
}
}
}
Complexity
Time Complexity
There are two implementations for this project. Each implementation has a different time complexity.
In both implementations, even though I halt Dijkstra's algorithm on finding the destination node, it is possible that every vertex will be deleted once. This yields a big O of (|V| * DeleteMin). Every vertex will need to be added and every edge may need to have its key value decreased, which yields a big O of ((|V| + |E|) * Insert or DecreaseKey) (Insert and DecreaseKey have the same big O).
My Array implementation has an overall big O of O(|V|2). The array priority queue has operations with the following complexities:
Insert(): O(1) (adding to an array is constant time)DeleteMin(): O(|V|) (the whole array must be searched to find the minimum key value)DecreaseKey(): O(1) (the array is not reordered after a key value is modified)The big O for the binary heap is therefore O(|V| * |V| + (|V| + |E|) * 1). The dominant term and final big O is O(|V| * |V|).
My Binary Heap implementation has an overall big O of O((|V| + |E|) log |V|) The binary heap priority queue has operations with the following complexities:
Insert(): O(log |V|) (bubbling up is at worst O(log n))DeleteMin(): O(log |V|) (bubbling down is at worst O(log n))DecreaseKey(): O(log |V|) (bubbling up is at worst O(log n))
The big O for the binary heap is therefore O(|V| * log |V| + (|V| + |E|) * log |V|). The dominant term and final big O is O((|V| + |E|) * log |V|).
Note: I kept an array of indices to nodes in the heap so I wouldn't have to traverse the heap in order to find the appropriate value when calling DecreaseKey. Instead, I simply looked up where the node was using my array of indices. This allows finding the node to be O(1) and the final big O of the function to be O(log n) with bubbling.
Space Complexity
My space complexity for both implementations is O(|V|). I used one array to store the vertices in my array implementation and two arrays to store the vertices in my binary heap implementation (one for the binary heap and one to store the references to points in the binary heap). The total time complexity of running either algorithm is only a constant multiple of O(|V|).
Outcomes
All times are measured in seconds.
Raw
Binary Heap
| 100 | 1,000 | 10,000 | 100,000 | 1,000,000 | |
|---|---|---|---|---|---|
| 1 | 0.0003 | 0.001 | 0.005 | 0.088 | 2.948 |
| 2 | 0.0001 | 0.001 | 0.014 | 0.376 | 5.410 |
| 3 | 0.0002 | 0.003 | 0.010 | 0.299 | 1.284 |
| 4 | 0.0001 | 0.001 | 0.007 | 0.282 | 6.517 |
| 5 | 0.0002 | 0.001 | 0.022 | 0.362 | 6.413 |
Array
| 100 | 1,000 | 10,000 | 100,000 | |
|---|---|---|---|---|
| 1 | 0.0001 | 0.008 | 0.193 | 28.293 |
| 2 | 0.0001 | 0.005 | 0.628 | 102.446 |
| 3 | 0.0001 | 0.011 | 0.423 | 88.876 |
| 4 | 0.0001 | 0.005 | 0.282 | 91.088 |
| 5 | 0.0001 | 0.010 | 0.892 | 99.778 |
Means
| 100 | 1,000 | 10,000 | 100,000 | 1,000,000 | |
|---|---|---|---|---|---|
| Binary Heap | 0.0002 | 0.001 | 0.012 | 0.281 | 4.514 |
| Array | 0.0001 | 0.008 | 0.484 | 82.096 | ~10000 |
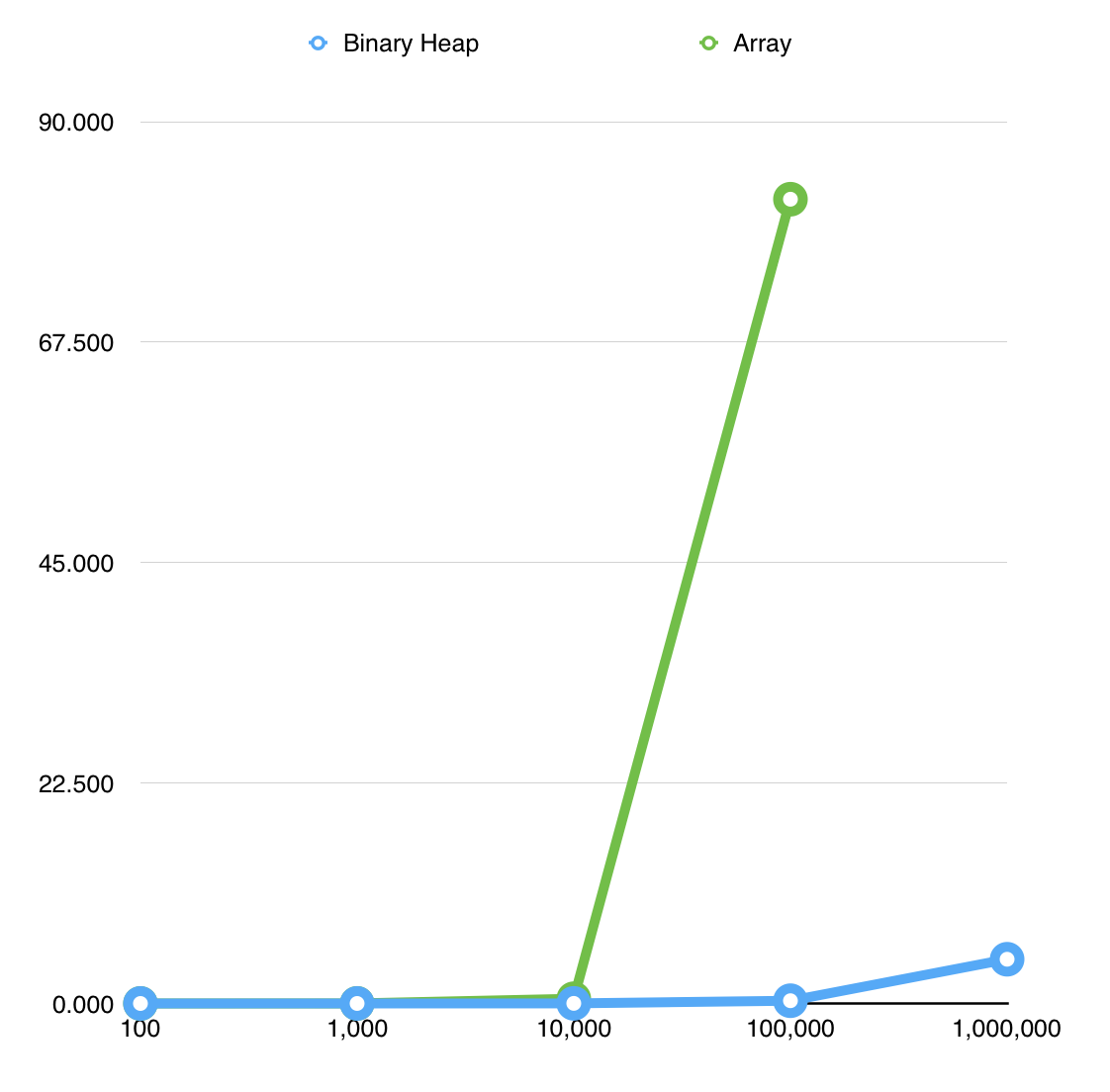
Graphs
I graphed the results in two different programs. 1,000,000 is omitted for the array implementation because I collected no data for it and it is easier to see the differences between the two graphs without it.

Discussion
The graphs of my results appear to be very skewed. It's difficult to see the O(n2) complexity for the array implementation as it doesn't seem to grow very quickly at first. The O(n log n) complexity for the binary heap implementation looks okay.
The actual values of the averages make it a little easier to see the correlation between the number of points and the time taken to find the shortest path. The binary heap grows a bit more quickly than if it had a linear slope and the array is certainly exponential. I tried to collect data for the array implementation at 1,000,000 points but I ran my program for more than an hour and the calculation still had not finished.
In general the results correlate with the expected outcomes of the two implementations. For small sets of points, the times to find the shortest path from one to another appear to be the same. However, with larger sets of points, the binary heap implementation of Dijsktra's algorithm is shown to be much more efficient than the painful array implementation.
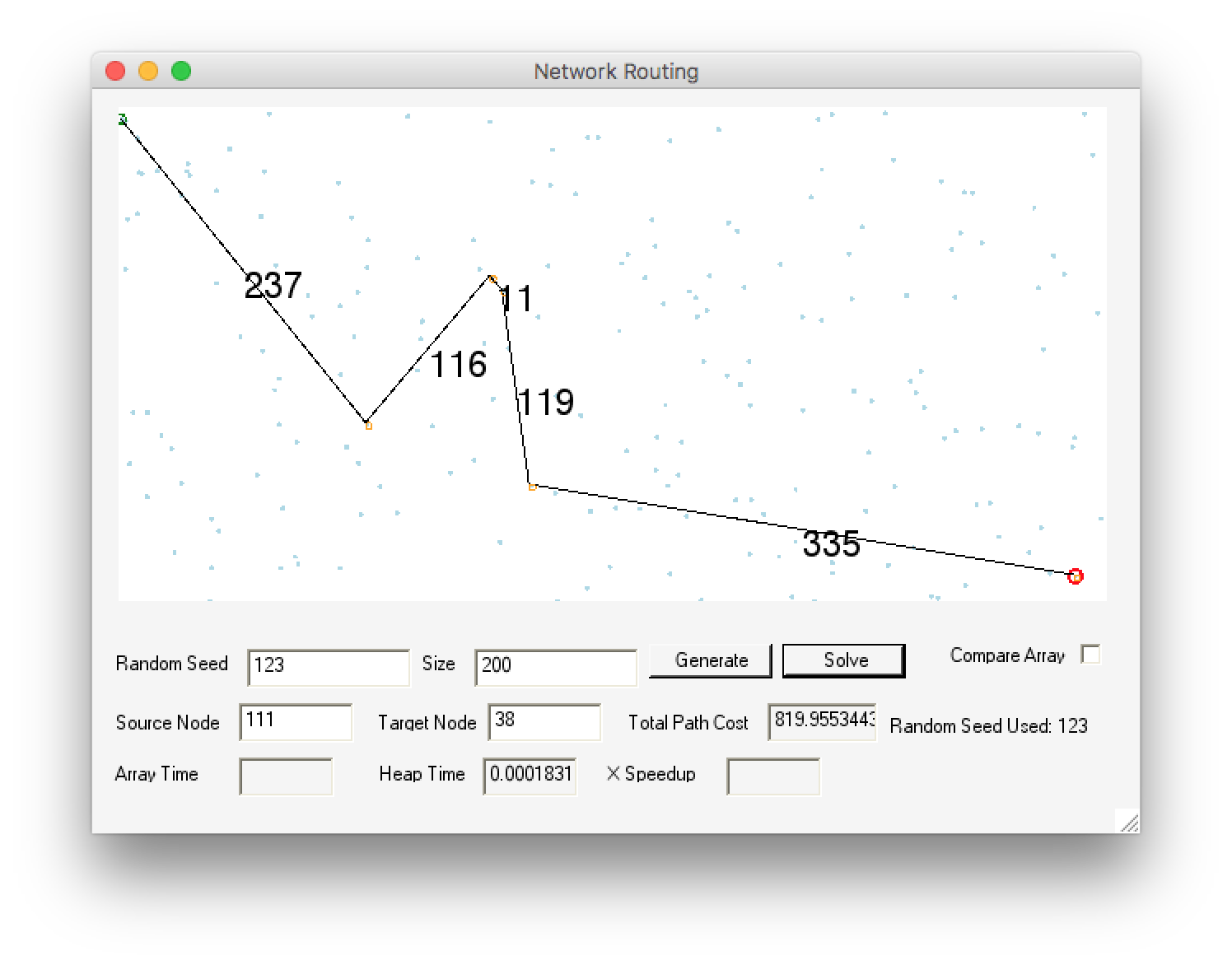
Screenshots
Note: as with many other students, my viewport was stretched in the Y direction. I tried to resize the viewport manually so as to match the size used in the example screenshots, but I may not have done so perfectly. Please keep that in mind if the Y values are off (or if distances appear more stretched the steeper a slope is).
Demo 1
Seed: 42, Size: 20, Source: 16, Destination: 17

Demo 2
Seed: 123, Size: 200, Source: 111, Destination: 38